«А в попугаях-то я гораздо длиннее!…» (м/ф 38 Попугаев)
Для ссылки в ваших публикациях на данный материал используйте:
Одейчук А.Н. Обобщенный критерий эффективности моделей прогнозирования временных рядов в информационных системах [Текст] / А.Н. Одейчук // Біоніка інтелекту: наук.-техн. журнал. – 2009. – № 1 (70). – С. 113-119
Существует достаточно большое количество критериев, применяемых для определения качества построенных моделей прогнозирования, их адекватности и точности.
Проведем краткий анализ возможностей использования этих показателей в качестве оценки эффективности модели.
Под эффективностью модели прогнозирования будем понимать набор количественных показателей, описывающих наиболее адекватную и оптимальную по своей структуре модель.
При анализе критериев использованы следующие обозначения:
Yt – значение временного ряда в момент t;
Ft – прогноз Yt;
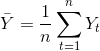
et=Yt-Ft – погрешность или ошибка прогноза;
n – длина временного ряда.
Наиболее часто встречаемые в литературе критерии эффективности приведены ниже.
Среднее абсолютное отклонение (Mean Absolute Derivation, MAD) измеряет точность прогноза, усредняя величину ошибки прогноза (абсолютные значения каждой ошибки) [1]. Использование MAD наиболее полезно в тех случаях, когда аналитику необходимо измерить ошибку прогноза в тех же единицах, что и исходный ряд. Ошибка MAD вычисляется с помощью следующего уравнения:
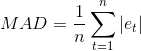
Однако недостатком данного критерия является нечувствительность к ошибкам, малым по абсолютной величине.
Среднеквадратическая ошибка (Mean Squared Error, MSE) и сумма квадратов ошибки (Sum Squared Error, SSE) рассчитываются по уравнениям, приведенным ниже.
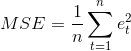
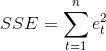
Данные критерии наиболее часто используются при выборе оптимальной модели прогнозирования в пакетах прикладных программ по прогнозированию [2]. Каждое значение ошибки прогноза в критериях (2) и (3) возводится в квадрат, что подчеркивает большие ошибки прогноза, в отличие от критерия (1). Данная особенность очень важна, так как модель прогнозирования, постоянно дающая средние по величине ошибки, в некоторых случаях может быть предпочтительнее другой модели, имеющей малые ошибки, но периодически дающей неприемлемые по абсолютной величине выбросы.
В тех случаях, когда проводится сравнение качества моделей прогнозирования разнородных объектов, оценка ошибок в абсолютных величинах не приемлема или вызывает трудности с интерпретацией получаемых результатов. В этой связи предпочтительным является переход к оценке ошибок в процентах [2, 3]. С этой целью используют среднюю абсолютную ошибку в процентах (Mean Absolute Percentage Error, МАРЕ) вычисляемую по уравнению:
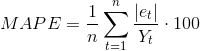
Этот показатель характеризует насколько велики ошибки прогноза в сравнении с действительными значениями ряда.
Более информативным критерием адекватности модели прогнозирования служит средняя процентная ошибка (Mean Percentage Error, МРЕ), определяющая смещенность (постоянное занижение или завышение) построенного прогноза [1, 4]. Данный критерий рассчитывается по уравнению:
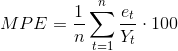
Значения, вычисляемые по уравнению (5), интерпретируются следующим образом. Если модель прогнозирования является несмещенной, критерий (5) будет иметь процентное значение, близкое к нулю и не должен превышать 5 % [2]. Если в результате расчетов получается большое отрицательное процентное значение, то построенная модель является последовательно переоценивающей. Если получено большое положительное процентное значение, то – последовательно недооценивающей.
Заметим, что критерии MAPE и MPE не подходят для временных рядов с нулевыми членами. Однако в работе [2] рекомендуют в таких случаях пропускать нулевые элементы ряда и уменьшать значение n на единицу.
Для целей определения адекватной модели прогнозирования применяют коэффициент несовпадения Тейла [4, 5], вычисляемый по уравнению:
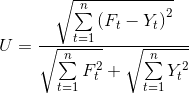
Если коэффициент принимает значение равное, нулю, то прогноз точный, а если значение, равно единице, то прогноз неадекватный.
Другим показателем адекватности модели может служить коэффициент детерминации (КД) [6, 7], который рассчитывается по уравнению:
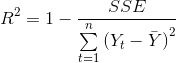
Чем ближе в выражении (8) значение КД к единице, тем лучше модель описывает реальные данные. На практике принято считать модель адекватной, если КД > 0,75 [6].
К недостаткам данного критерия, а также коэффициентов (1 – 7) можно отнести то, что их значения тем больше свидетельствуют об улучшении точности модели, чем больше новых параметров включается в модель, хотя это и не обязательно означает улучшение качества модели. Учесть данную особенность позволяет скорректированный коэффициент детерминации (СКД) [8, 9], где r – количество параметров модели:
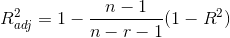
СКД построен таким образом, что добавление нового параметра в модель приводит к снижению его значения – штрафуется [10]. Эта особенность выгодно отличает СКД от критериев (1 – 7), которые фокусируют внимание исследователя на величине отклонения прогноза от реальных данных и не учитывают степень оптимальности структуры построенной модели.
Тем не менее, близкое к единице значение КД и СКД еще не свидетельствует о хороших прогнозных качествах модели: необходимо отсутствие автокорреляции ошибок, что может быть проверено с помощью статистики Дарбина-Уотсона. Однако она не применима, если в модели среди объясняющих переменных имеются лаговые значения результативного признака. В этой связи предлагается использовать Q-статистику Льюнга-Бокса (Ljung-Box Q-statistic, LBQ), имеющую распределение Хи-квадрат и рассчитываемую по формуле [10]:
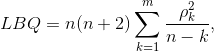
где
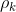
– значение автокорреляционной функции.
Если Q-статистика больше заданного квантиля распределения Хи-квадрат, то признается наличие автокорреляции до m-го порядка в исследуемом ряду.
Также следует отметить, что критерий СКД может принимать значения больше единицы и отрицательные значения (пример приведен в (10)), что не дает возможности корректно интерпретировать данный критерий.
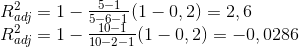
На принципе штрафов за дополнительные параметры построены критерии Маллоуза, Акаике и Шварца [1, 8, 11, 12].
Критерий Маллоуза
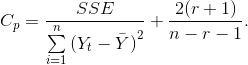
Информационный критерий Акаике
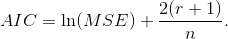
Байесовский информационный критерий (критерий Шварца)
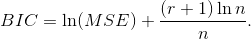
Модель прогнозирования тем лучше, чем ниже показатель Cp, AIC, BIC. На данные критерии положительно влияет уменьшения остаточной дисперсии и отрицательно – количество включенных параметров. Основным различием между ними является степень жесткости, то есть, насколько велик штраф за большое количество параметров в модели.
Критерии Cp и AIC при больших n сильно коррелированны между собой. Однако Cp несколько жестче AIC, особенно при малых n. BIC является наиболее жестким критерием, причем, как можно увидеть из приведенной формулы (13), в отличие от остальных критериев, его жесткость возрастает с ростом n.
Различие в жесткости проистекает из различия в предъявляемых требованиях к моделям прогнозирования. Критерии Cp и AIC направлены на достижение высокой точности прогноза: Cp направлен на минимизацию дисперсии ошибки прогноза, а AIC – на минимизацию расхождения между плотностью распределения по истинной модели и по выбранной модели. В основе критерия BIC лежит требование максимизации вероятности выбора истинной модели.
Кроме того, следует отметить существенный недостаток критерия Акаике, состоящий в переоценке истинного количества параметров в модели [13]. В свою очередь критерий Маллоуза применим только при нормальном распределении остатков [14].
При сравнении моделей прогнозирования важно учитывать, что если разные модели используют различные функциональные формы, то нельзя непосредственно сравнивать КД, СКД или значения критериев (1-7). Например, нельзя сравнить эти статистики для линейного и логарифмического варианта модели.
Значения, получаемые по логарифмической модели значительно меньше соответствующих значений линейной модели, поэтому является естественным, что остатки также значительно меньше. Величина КД безразмерна, однако в двух уравнениях она относится к разным статистическим понятиям. В одном уравнении она измеряет объясненную моделью долю дисперсии зависимой переменной, а в другом – дисперсии логарифма зависимой переменной. Для сопоставимости значений критериев в работе [7] рекомендуется применение процедуры Бокса-Кокса. Данная процедура предполагает преобразования масштаба наблюдений зависимой переменной, при котором обеспечивалось бы возможность непосредственного сравнения суммы квадратов отклонений.
Проведенный сравнительный анализ критериев эффективности моделей прогнозирования показал, что для непосредственной оценки адекватности и точности модели прогнозирования могут быть использованы критерии (2-4, 6, 7).
Критериями, которые позволяют учитывать помимо адекватности модели степень оптимальности ее структуры, выражаемую через количество включенных в модель прогнозирования параметров, являются критерии, представленные в уравнениях (8, 11-13). На основе анализа их недостатков и ограничений наиболее предпочтительным при сравнении моделей является критерий (13). Это связанно с тем, что данный критерий помимо того, что учитывает адекватность и степень сложности структуры модели, также ориентирован на минимизацию ошибки выбора структуры модели прогнозирования, что наиболее полно отвечает требованиям поставленной задачи. Результаты исследований, приведенные в работе [17], свидетельствуют о том, что критерии MAD, MSE и MPE дают согласованные результаты, а критерии КД, СКД, Cp, AIC и BIC не противоречат друг другу [10].
Литература
1. Ханк Д.Э., Уичерн Д.У., Райс А. Дж. Бизнес-прогнозировнаие, 7-е издание.: Пер. с англ. – М.: Издательский дом «Вильямс», 2003. – 656 с.
2. Льюис К.Д. Методы прогнозирования экономических показателей / Пер. с англ. и предисл. Е.З. Демиденко. – М.: Финансы и статистика, 1986. – 133 с.
3. Ярова В.В. та ін. Економетрика: Лекції / Ярова В.В., Александрова А.І. / Харк. Нац.. аграр. Ун-т ім.. В.В. Докучаєва. – Х., 2003. – 124 с.
4. Чернышев С.Л. Моделирование экономических систем и прогнозирование их развития: Учебник. – М.: Изд.-во МГТУ им. Н.Э. Баумана, 2003. – 232 с.
5. Уразаев Р.П. Методы генерации алгоритмов прогнозирования при помощи операций над базовыми алгоритмами. – М.: Вычислительный центр АН СССР, 1988. – 25 с.
6. Демиденко Е.З. Линейная и нелинейная регрессия. – М.: Наука, 1987. – 248с.
7. Ежеманская С.Н. Эконометрика / Серия «Учебники, учебные пособия». – Ростов н/Д: Феникс, 2003. –160 с.
8. Арженский С.В., Федосова О.Н. Эконометрика: Учебное пособие. – Ростов н/Д.: Рост. Гос. Экон. Унив., 2002. – 102 с.
9. Княженко І.І., Павленко Л.В. Економетрія: Навчально-методичний посібник. – Донецьк: ТОВ «Юго-восток, Лтд», 2006. – 187 с.
10. Суслов В.И., Ибрагимов Н.М., Талышева Л.П., Цыплаков А.А. Эконометрия. – Новосибирск: Издательство СО РАН, 2005. –744 с.
11. Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс: Учеб. – 6-е изд., перераб. и доп. – М.: Дело, 2004. – 576 с.
12. Грін, Вільям Г. Економетричний Аналіз / Пер. з англ. А.Олійник, Р.Ткачук.; Наук. ред. пер. О.Комашко; Передм. О.І.Черняка, О.В.Комашка. – К.: Видавництво Соломії Павличко «Основи», 2005. – 1197 с.
13. Носко В.П. Эконометрика: Введение в регрессионный анализ временных рядов. — М.: МФТИ, 2002. — 273 с.
14. Стадник М.П. Модификация критерия Мэллоуза-Акаике для подбора порядка регрессионной модели / Автоматика и техника. – 1988. – №4. – С. 98–108.
15. Makridakis S., Hibon M. The M-3 Competition: Results, Conclusions and Implications. International of Forecasting, 16 (2000), 451-476.