Нейронная сеть Хопфилда

Область применение:
Ассоциативная память, распознавание образов, оптимизационная комбинаторика. 

Архитектура:
Сеть Хопфилда – это искусственная нейронная сеть без входов, содержащая один рекуррентный слой с шаговой (симметрично линейной с ограничениями) функцией активации (наиболее часто используется сигнум-функция.

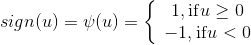
Обучение (формирование матрицы синаптических весов)

Выполняется по модифицированному правилу Хэбба, учитывающего тот факт, что элементы главной диагонали матрицы синаптических весов должны быть нулевыми. Для этого используются целевые вектора-столбцы, которые описывают состояния равновесия системы. Это могут быть, например, образы, которые мы желаем, чтобы нейронная сеть Хопфилда распознавала в дальнейшем. Образы должны быть представлены в векторной форме в симметричной системе счисления. 

Рассмотрим, например, N = 3 целевых вектора состояний. 

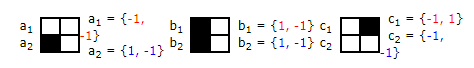
Результирующие целевые вектора состояний, описывающие образы для распознавания, будут иметь следующий вид. Длина каждого из векторов n = 2*2 = 4. 

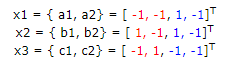
Выражение для задания матрицы синоптических весов нейронов имеет следующий вид:

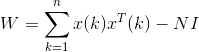
или в матричном виде 

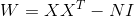
Иногда, выражение (2) нормируется на размерность входного пространства, что придает синаптическим весам сети смысл коэффициентов взаимной корреляции: 

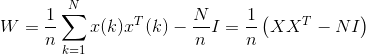
Для рассматриваемых нами целевых векторов x1, x2, x3 матрица весов используя выражение (3) будет равна

X_4×3 = { x1, x2, x3}

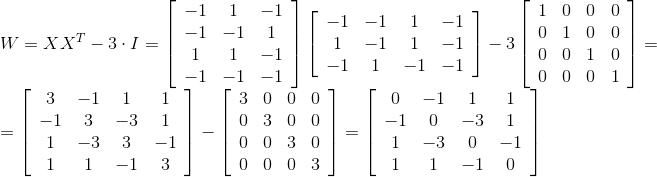
Алгоритм работы нейронной сети Хопфилда в синхронном режиме:

1. Подготовка образов, которые должна будет распознавать нейронная сеть Хопфилда.
2. Задание матрицы синоптических весов по выражению (3).
3. Для распознавания вектора Y, размером n×1, используется следующее выражение:

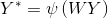
4. Если Y*не равен Y, то Y=Y* и переход к шагу 3, в противном случае завершение работы. 

Максимально количество образов, которые может запомнить нейронная сеть Хопфилда рассчитывается по формуле 

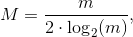
где m = n*n – количество нейронов в сети. 

Пример работы алгоритма работы сети Хопфилда

1. Образы: x1, x2, x3.
2. Расчет матрицы синоптических весов W представлен выше.
3. Допустим вектор, который мы хотим, чтобы распознала нейронная сеть Хопфилда, зашумлен и имеет вид 

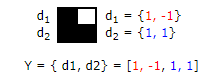
Тогда 

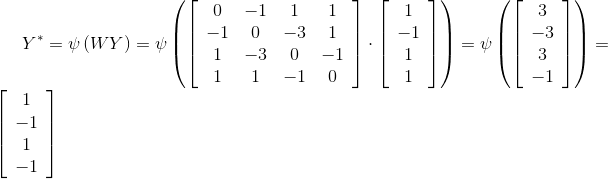
4. Учитывая, что Y*≠Y, то приравниваем полученное значение Y* переменной Y и повторяем шаг 3. 

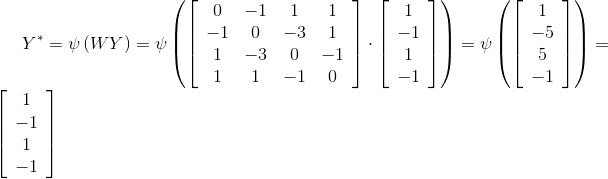
5. Неравенство Y*≠Y не выполняется, поэтому алгоритм распознавания образа завершен. Распознанный образ ассоциирован нейронной сетью Хопфилда с вектором x₂. 

Обозначения:
x(k) – (n×1) – вектор состояний
W – (n×1) – матрица синоптических весов
N – объем обучающей выборки
M – максимальное количество образов, которые может запомнить нейронная сеть
m – количество нейронов в сети
I – (n×n) – единичная матрица
ψ – сигнум-функция. 

Листинг программы на языке MatLab реализующий нейронную сеть Хопфилда

clear all;
clc;
% Целевые вектора
x1 = [ -1, -1, 1, -1]’;
x2 = [ 1, -1, 1, -1]’;
x3 = [-1, 1, -1, -1]’;
% Матрица целевых векторов
X = [x1, x2, x3];
% Матрица синоптических весов
W = X * X’ — size(X,2) * eye( size(X,1), size(X,1) );
% Вектор для распознавания
y = [1, -1, -1, 1]’;
% Цикл для распознавания
isStop = false;
yOld = y;
t = 0; tMax = 100; % Счетчик и максимальное количество попыток распознавания
while isStop == false
   y = signFun(W * yOld);
   if y == yOld
      isStop = true;
   else
      yOld = y;
      t = t + 1;
      if t > tMax, isStop = true; end;
   end;
end;
% Вывод результатов
if t <= tMax
   disp(‘Распознавание образа завершено.’);
   disp(‘Распознанный образ:’);
   disp(y);
else
   disp(‘К сожалению, распознать образ не удалось.’);
end;