Теория принятия решений является фундаментом науки исследования операций. Любой процесс принятия решения содержит такие элементы:
– лицо, которое принимает решение (ЛПР);
– множество переменных, значение которых выбирает ЛПР, это управляемые переменные, управление или стратегии;
– множество переменных, которые зависят от выбора стратегий, их называют следствиями решений;
– множество переменных, значение которых не регулируется ЛПР;
– ограничение на управление и исходные переменные;
– целевая функция (критерий оптимальности), с помощью которой оцениваются свойства решения;
– математическая модель задачи принятия решения.
Задачи, которые являются объектом математических методов, это, как правило, задачи на нахождение экстремальных значений некоторых функциональных зависимостей. Каждая операция проводится для достижения определенной цели. В идеальном случае степень ее достижения и вся совокупность действий, которые происходят в операции и от которых зависит достижение цели, имеют количественную меру, т.е. могут быть описанные математически. Некоторые из таких количественных характеристик бывают неизменными, постоянными для определенной операции или определенных условий. Обозначим их
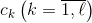
Это и есть параметры задачи. Другие имеют характер переменных величин, независимых и зависимых, детерминированных или случайных. Независимые переменные можно поделить на две группы: управляемые, значение которых можно изменять
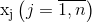
неуправляемые, значения которых Определяются комплексом внешних условий (внешним окружением), или параметры системы
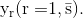
При таких условиях, как правило, удается установить функциональную зависимость между некоторой величиной Z, которой измеряют степень достижения цели, и независимыми переменными и параметрами операции
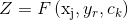
Функция (1.1) есть целевой или критерием оптимальности, поскольку ее значение является мерой эффективности проведения операции после достижения Определенной цели.
Задача состоит в том, чтобы выбрать такие значения управляемых переменных xj, которые бы предоставляли целевой функции экстремального значения, т.е.
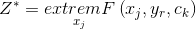
Тем не менее возможности выбора управляемых переменных xi всегда ограниченные внешними относительно операции условиями (энергетическими, материальными, человеческими, денежными ресурсами и т.п.), а также параметрами самой операции. В идеальном случае ограничения можно описать системой математических равенств и неровностей:
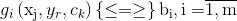
Зависимости (1.3) называют системой ограничений, или системой условий задачи.
Выражения (1.1) и (1.3) и является математической моделью операции.
Таким образом, задача заключается в том, чтобы найти
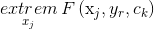
при условиях
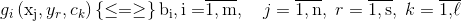
где F() – целевая функция (показатель качества или эффективности операции); gi(), bi – соответственно функция затраты и величина i-го ресурса.

