С того момента как был предложен первый искусственный нейрон в 1943 году У. Маккалохом и У. Питтсом и в качестве активационной функции (передаточной функции) был использован бинарный ограничитель было предложено использовать множество других.
Функция активации нейрона, как правило, выбирается из класса сигмоидальных (S-образных) функций — непрерывных функций, имеющих две горизонтальные асимптоты и одну точку перегиба. Областью существования передаточных функций является вся числовая ось, а множество значений определяется диапазоном значений базовой функции.
Основные виды активационных функций.
Функция Хэвисайда
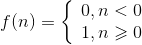
Линейная функция
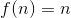
Положительно линейная (полулинейная) функция
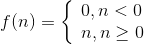
Линейная с ограничениями функция
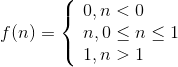
Симметричная линейная с ограничениями (шаговая) функция
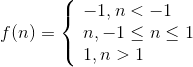
Симметричная с жесткими ограничениями (знаковая) функция
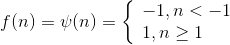
Треугольная функция
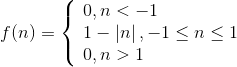
Экспоненциальная (радиальная) функция
Функция
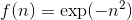
Производная
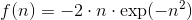
Логистическая функция
Функция
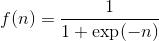
Производная
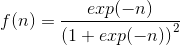
Гиперболическая тангенциальная функция
Функция
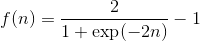
Производная
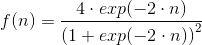
Синусоидальная функция
Функция
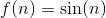
Производная
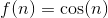
Рациональная (гиперболическая) функция
Функция
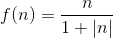
Производная
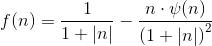
Модульная функция
Функция
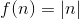
Производная
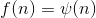
Квадратичная функция
Функция
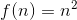
Производная
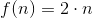
Каждая пороговая функция из представленных выше порождает целый класс функций активации, если в аналитическое представление ее ввести числовые параметры.
Например, экспоненциальная функция
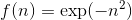
записанная в виде
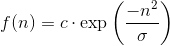
где с, σ — константы (числовые параметры), дает семейство так называемых гауссовых функций.

