Прогнозирование с помощью скользящих средних достаточно распространенный подход. Несмотря на свою простоту, он позволяет получить неплохие результаты даже при малом количестве данных.
Основными методами, основанными на скользящих средних, являются: простое экспоненциальное сглаживание, взвешенное скользящее среднее, модель Хольта, модель Хольта-Уинтерса. Вот о них как раз и пойдет речь ниже.
Простое экспоненциальное сглаживание
Экспоненциальное сглаживание — это очень популярный метод прогнозирования многих временных рядов. Исторически метод был независимо открыт Броуном и Холтом. Простая и прагматически ясная модель временного ряда имеет следующий вид:
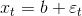
где b — константа
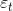
– случайная ошибка.
Константа b относительно стабильна на каждом временном интервале, но может также медленно изменяться со временем. Один из интуитивно ясных способов выделения b состоит в том, чтобы использовать сглаживание скользящим средним, в котором последним наблюдениям приписываются большие веса, чем предпоследним, предпоследним большие веса, чем пред-предпоследним и т.д. Простое экспоненциальное именно так и устроено. Здесь более старым наблюдениям приписываются экспоненциально убывающие веса, при этом, в отличие от скользящего среднего, учитываются все предшествующие наблюдения ряда, а не те, что попали в определенное окно. Точная формула простого экспоненциального сглаживания имеет следующий вид:
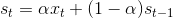
Когда эта формула применяется рекурсивно, то каждое новое сглаженное значение (которое является также прогнозом) вычисляется как взвешенное среднее текущего наблюдения и сглаженного ряда. Очевидно, результат сглаживания зависит от параметра α (Альфа)
Если α равно 1, то предыдущие наблюдения полностью игнорируются.
Если α равно 0, то игнорируются текущие наблюдения.
Значения α между 0, 1 дают промежуточные результаты.
Эмпирические исследования Makridakis и др. показали, что весьма часто простое экспоненциальное сглаживание дает достаточно точный прогноз.
Предположениями данного метода является, что математическое ожидание ошибки равно нулю.
Взвешенное скользящее среднее
Применяя скользящую среднюю для выравнивания исходного ряда наблюдений, заменяются значения уровня у в середине интервала усреднения на его среднее у (простое или взвешенное). При этом коэффициенты для скользящей средней вычисляются из условия минимизации суммы квадратов отклонений уровней от значений выбираемого сглаживающего полинома
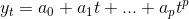
Значение средней yt выражается через
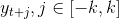
по формуле:
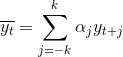
где
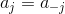
Это значение можно принять как прогноз уровня yt в момент t. При этом в предположении, что уt являются случайными некоррелированными величинами с дисперсией
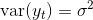
, можно оценить дисперсию, а затем оценить ошибку с заданным уровнем доверия.
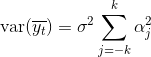
Из этого примера видно, что дисперсия усредненного значения, а следовательно и ошибка восстановленного значения, быстро растет с увеличением отклонения от центра усреднения. Несмотря на это, правомерно будет использовать получаемый полином для прогнозирования, т.е. получения прогнозных значений уровней для моментов времени j=k+l,k+2,…. Если при этом взять центр интервала сглаживания в точке t=n-k, то получим прогнозные значения уровней вне интервала наблюдений, т.е.
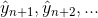
Для оценки дисперсии прогнозного значения уровни должны являться случайными независимыми величинами с постоянной дисперсией.
Модель Хольта
В модели Хольта параметры a0(t) и a1(t) для аддитивной модели
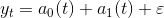
оцениваются с помощью двух скользящих средних, имеющих различные независимые параметры сглаживания.
Коэффициент a1(t) оценивается как экспоненциальная средняя приростов параметра a0(t).
Введя обозначение для прироста параметра a0(t) в момент t получим:
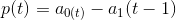
Тогда согласно модели Хольта:
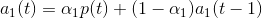
где
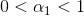
— первый параметр сглаживания.
Коэффициент a0(t) есть экспоненциальная средняя уровней ряда, вычисленная с учетом поправки на предыдущий прирост a1(t-1):
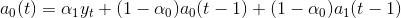
где
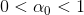
— второй параметр сглаживания не зависящий от α 1
Прогноз в момент t на L шагов вперед осуществляется по формуле
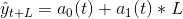
Если обозначить ошибку прогноза, сделанного в момент t-1 на момент t через еt т. е.:
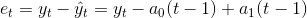
то
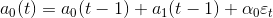
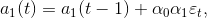
которые можно использовать для поправки прогнозов при получении дополнительных данных.
В модели Хольта, таким образом, используется два независимых параметра сглаживания а0 и ап. Рекомендуют использовать
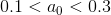
и
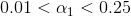
Значение а0(0) следует выбрать как среднее нескольких начальных значений уровней ряда, а значение a1(0) как среднее нескольких начальных значений первых разностей уровней.
Модель Хольта-Уинтерса
Уинтерс обобщил модель Хольта для случая, когда ряд имеет сезонную составляющую, при этом рассматривается аддитивно-мультипликативная модель, где сезонная компонента входит мультипликативно:
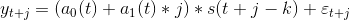
где k – период сезонности, s(t+j–k) – множитель, учитывающий сезонный эффект (коэффициент сезонности, сезонная компонента). Все три компоненты a0(t), a1(t) и s(t) вычисляются как экспоненциальные средние.