Матрицы, транспонирование матриц (Основы нейронных сетей)

Изучение систем нелинейных обыкновенных дифференциальных уравнений, дифференциальные уравнения, линейная алгебра и нелинейное программирование являются фундаментальными для анализа и синтеза искусственных нейронных сетей.

Прежде всего следует остановится на такой теме как матрицы и вектора и дать основные определения.

Матрицей это система элементов (в частном случае чисел), расположенных в определенном порядке и образующих таблицу. Если в этой таблице m строк и n столбцов, а ее элементы обозначены как a_ij, где i — номер строки, а j — номер столбца, на пересечении которых находится этот элемент, то матрица записывается в следующем виде:

A = \left[ {\begin{array}{*{20}{c}} {{a_{11}}}&{{a_{12}}}&{{a_{13}}}&{...}&{{a_{1n}}}\\ {{a_{21}}}&{{a_{22}}}&{{a_{23}}}&{...}&{{a_{2n}}}\\ {...}&{...}&{...}&{...}&{...}\\ {{a_{m1}}}&{{a_{m2}}}&{{a_{m3}}}&{...}&{{a_{mn}}} \end{array}} \right]

Матрица A может быть компактно записана как

$A = {\left[ {{a_{ij}}} \right]_{m \times n}}$

Матрица имеет размер m x n, где m – количество строк, n – количество столбцов.

Матрица размером m x 1 называется вектором-столбец и 1 x n называется вектором-строкой.

Поэтому A, если это вектор-строка, может быть записана в виде:

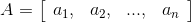
Транспонирование матриц

Транспонирование любой матрицы выполняется переписыванием всех столбцов как строк. Транспонирование матрицы A обозначается A^T. Результатом транспонирования матрицы m x n является матрица n x m, где (i,j)-й элемент это a_ij. Таким образом, справедливо (A^T)^T=A и (AB)^T = B^TA^T.

Симметричные, диагональные и единичные матрицы

Пусть A это n x m матрица. Если A = A^T, тогда A называется симметричной.

Если все элементы матрицы равны нулю, кроме элементов на главной диагонали, то такая матрица называется диагональной:

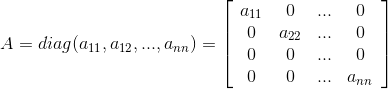
Матрицы, транспонирование матриц (Основы нейронных сетей)

Единичная матрица – это диагональная матрица, все диагональные элементы которой равны единице. Единичная матрица n x n обозначается I_n, либо просто I.