Область применение: прогнозирование, сжатие информации, ассоциативная память, классификация.
Архитектура: Обычный многослойный персептрон это нейронная сеть прямого распространения с нейронами расположенными в слоях. Как правило, все нейроны в слоях соединены со всеми нейронами в соседних слоях однонаправленными соединениями. Эти соединения характеризуются синоптическими весами. Синоптические веса умножаются на сигналы соответствующих соединений. Внутри слоя нейроны не соединяются.
Например, в трехслойном персептроне, схематически изображенном на рисунке 1. нейроны сгруппированы в последовательно соединенные слои. Каждый слой номеруется от 0 до 3. Нейроны 0 слоя (иногда называемого слоем входов) не выполняет расчетов, а только передает входные сигналы нейронам 1 слоя, который называется первый скрытый слой. Последний слой (3 слой) – это слой выходов. Слои нейронов между слоями входов и выходов называются скрытыми слоями.
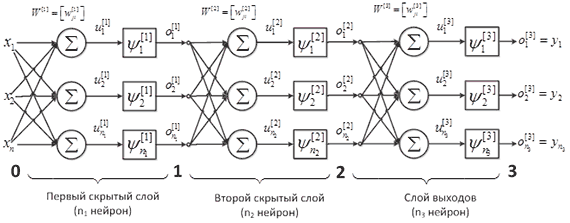
Вообще, теоретически слоев может быть неограниченное количество, но обычно на практике бывают только один или два скрытых слоя. Доказано, что достаточно использовать максимум три слоя (два скрытых и один слой выходов).
Стрелками показывается направление передачи информации (сигнала). Вообще, в многослойном персептроне количество нейронов может отличаться в различных слоях. Каждый нейрон в многослойном персептроне характеризуется одним выходом и множеством входов, которые соединены с выходами нейронов предыдущего слоя.
Пусть uj – это значение сигнала от j-го нейрона находящегося в s-слое (s=1,2,3) (Рис. 1). Взвешенная сумма входов вычисляется для соответствующего нейрона следующим образом:
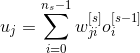
где
s=1,2,3;
j=1,2,…,ns;
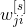
— вес синапса, который в j-м нейроне умножается на входящий сигнал;
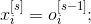
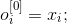
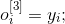
ns — это число нейронов в s-слое.
Значение, получаемое на выходе нейрона, вычисляется путем расчета нелинейной активационной функции
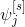
от взвешенной суммы входов нейрона
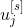
, т.е.
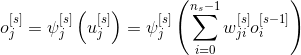
Каждый слой сети может быть представлен нелинейной матрицей операторов:
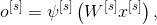
где
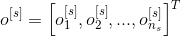
– это вектор значений на выходе;
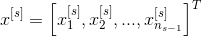
– это вектор значений на выходе;
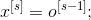
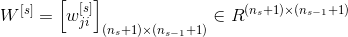
– это матрица весов в s-слое;
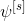
– диагональный нелинейный оператор сигмоидальных активационных функций (обычно во всех слоях используется одна и та же функция).
Таким образом, схема преобразования входа в выход в трехслойном персептроне может быть представлена в компактной матричной форме:
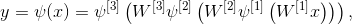
Блок схема данного преобразования представлена на рисунке 2.
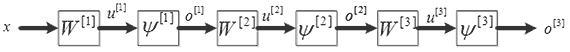
Обычно нейроны функционируют в нормированном диапазоне от +1 до -1 (в некоторых приложениях диапазон может быть от +1 до 0).
Также следует отметить, что синоптические веса предопределяют поведение сети. Их значения задаются до проведения расчетов с помощью процедуры обучения. Затем они являются константами (фиксированными) на протяжении всех вычислений.
Процесс обучения многослойного персептрона выполняется в обратном порядке относительно слое. Вначале обучается последний слой, а в конце обучения – первый скрытый слой.

