Симплекс-метод состоит в таком направленном переборе вершин, при котором значение целевой функции возрастает от вершины к вершине. Каждой системе соответствует система уравнений, выбираемая специальным образом из системы неравенств
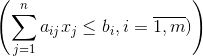
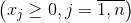
поэтому вычислительная процедура симплексного метода состоит в последовательном решении систем линейных уравнений. Простота алгоритма делает этот метод удобным для его реализации на ЭВМ.
План решения задачи симплекс-методом
1. Математическая формулировка задачи
2. Нахождение 1-го базисного решения (опорного плана) Т.к. симплекс-метод направлен на решение задач в каноническом виде, то для перехода от неравенств необходимо ввести дополнительные неотрицательные переменные. После чего каждую из них выразить из каждого полученного уравнения и приравняв все другие переменные нулю.
3. Переход к 1-ой симплексной таблице

4. Последовательное улучшение решения (плана) или переход от 1-ой симплексной таблицы ко второй, от 2-ой таблицы к 3-ей и т.д. вплоть до получения последней симплексной таблицы.
5. Выписка оптимального решения (плана) и величины функции цели из последней симплексной таблицы.

