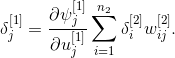Архитектуру многослойного персептрона мы рассматривали ранее. Теперь рассмотрим стандартный алгоритм обучения обратного распространения для многослойного персептрона.
Для упрощения в дальнейшем будем рассматривать трехслойный персептрон: первый скрытый слой с n0 входами и n1 элементами, второй скрытый слой с n2 элементами и выходной слой с n3 элементами (Рисунок 1).
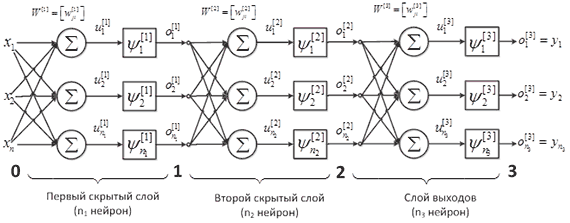
Обучение многослойного персептрона является специфической задачей эквивалентной поиску значений всех синоптических весов таких, чтобы желанный выход генерировался при соответствующем входе. В более строгом виде, обучение многослойного персептрона заключается в определении всех его весов так, чтобы ошибка изменения между определяемым выходом djp и имеющийся выходной сигнал yjpв среднем по всем p обучающим примерам будет минимальна (равна нулю).
Стандартный алгоритм обратного распространения использует дискретный пошаговый градиентный подход минимизации функции среднеквадратической ошибки. Так (локальная) функция ошибки для p примеров обучения может быть представлена в виде
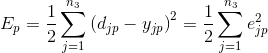
и глобальная (общая) функция ошибки как
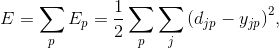
где djp и yjp — определяемый и имеющийся выходные сигналы для p образцов (обучающих примеров) j-го нейрона в выходном слое.
Имеется два основных подхода для поиска минимума общей ошибки функции E.
Первый подход – это последовательное представление обучающих примеров (в реальном времени), обычно в произвольном порядке. Для каждого обучающего примера синаптические веса
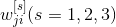
изменяются на величину
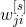
пропорциональную соответствующему отрицательному значению градиента локальной функции ошибки Ep, которое может быть записано как
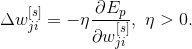
Доказано, что если параметр обучения
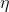
достаточно мал, эта процедура минимизирует функцию общей ошибки
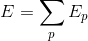
Общее правило градиентного спуска в дискретном виде может быть представлено в виде непрерывного дифференциального уравнения
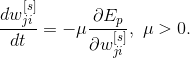
Во втором подходе, иногда называемый «пакетное обучение», минимизация функции общей ошибки E ведется таким способом, что изменения весов накапливаются для всех обучающих примеров, перед тем как будет выполнено изменение весов.
Мы рассмотрели подход обучения в реальном времени, в котором градиентный поиск и пространстве синаптических весов выполняется с использованием функции локальной ошибки Ep. Запишем выражение для синаптических весов
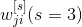
слоя выходов используя цепное правило.
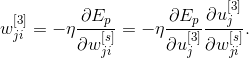
Принимая во внимание, что
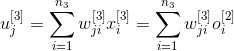
и определение локальной ошибки, называемой дельта
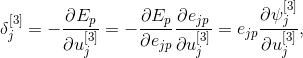
мы получим общую формулу для изменения весов в слое выходов
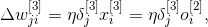
где
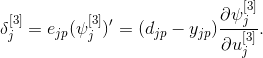
Изменение синоптических весов в скрытых слоях выполняется немного сложнее. Для второго скрытого слоя мы можем записать
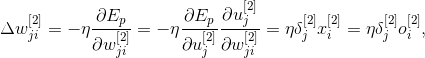
где локальная ошибка для второго скрытого слоя определяется как
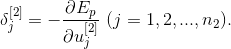
Однако, данная локальная ошибка не может быть непосредственно определена, как это сделано для локальной ошибки слоя выходов. Вместо этого, попытаемся выразить, через величину (сигнал), которая уже известна, и другие величины, которые легко определить.
Используя цепное правило, можем записать
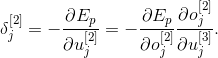
Учитывая, что
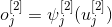
имеем
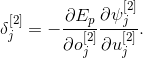
Выражение
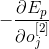
можно определить как
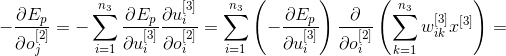
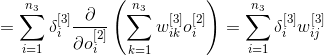
Таким образом, локальная ошибка второго слоя можно определить используя следующую формулу
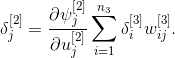
Аналогичным образом, можем записать выражение для первого скрытого слоя
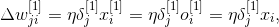
где