Для обучения однослойного персептрона обычно применяется алгоритм обратного распространения. Рассмотрим его принцип работы более подробно на примере одного нейрона выходного слоя персептрона.
Предположим, что нелинейная активационная функция нейрона задается функцией гиперболического тангенса, а именно
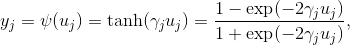
где
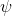
– нелинейной активационной функции;
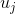
–значение сигнала от j-го нейрона;
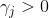
Целью обучения является минимизация квадрата ошибки выходного сигнала изменяя синаптические веса wji.
Постановку задачи для обучения можно сформулировать следующим образом.
Дано множество синоптических весов wji и смещение —
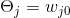
Необходимо найти насколько требуется увеличить или уменьшить синаптические веса, чтобы уменьшить ошибку задаваемую функцией Ej. Это может быть сделано, используя правило градиентного наискорейшего спуска задаваемое выражением
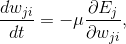
где
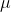
– это положительный параметр обучения, определяющий скорость приближения к минимуму.
Учитывая, что ошибка
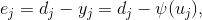
где
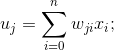
wji – вес синапса, который в j-м нейроне умножается на входящий сигнал xi;
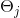
— смещение j-го нейрона;
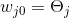
x0=1.
Применим цепное правило.
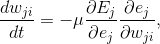
Получим
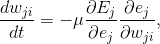
где
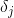
— называется обучающим сигналом или локальной ошибкой, определяемой как
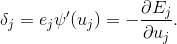
Если в качестве сигмоидальной функции активации выбрана функция гиперболического тангенса (1), тогда производная
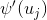
будет равна
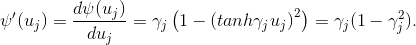
В этом случае выражение (2) может быть записано
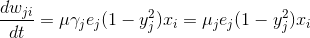
где
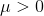
Заметим, что изменения весов выполняется стабильно, если yj приблизительно -1 или +1, поскольку производная
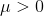
, равна
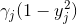
, достигая своего максимума при yj=0 и минимума при
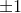
Синаптические веса обычно изменяются с определенным шагом и постепенно сходятся к тем значениям, которые позволяют решить поставленую задачу. В основе алгоритма положено выражение (2), которое с шагом (при дискретном времени) изменяет веса wji. Шаг можно записать в виде
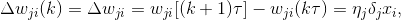
где
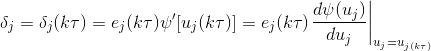
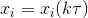
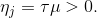
Обычно
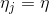
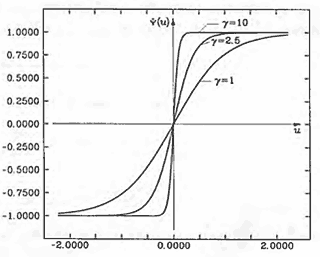
Реализация всего алгоритма требует точного знания сигмоидальной функции и ее производной. График этих функций для различных значений параметра
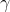
изображен на рисунке 1. Заметим, что форма и значения экстремумов производной сигмоидной нелинейности строго зависят от значений параметра
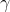
(см. рис. 2).