Регрессионный анализ (Метод наименьших квадратов)

Регрессионный анализ относится к статистическим методам анализа и обработки данных. Он широко применяется для построения математических зависимостей по экспериментальным данным, когда одна переменная зависит от значений других переменных. 

История развития регрессионного анализа началась с 1805 года, когда А.М. Лежандромом был предложен метод наименьших квадратов. Понятие «регрессия» было впервые упомянуто в 1885 году Франсисом Гальтоном. Регрессионной связью называется связь между переменными, в которой ожидаемое значение одной зависимой (прогнозируемой, регрессионной) переменной взаимосвязана с другими независимыми (предикторами, регрессорами, аргументами регрессии) переменными:

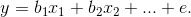
Для корректного использования регрессионного анализа, в частности метода наименьших квадратов (МНК) существуют следующие допущения на свойства регрессионной ошибки 

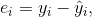
где

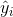
– оценка значения зависимой переменной.

Допущения: 

1. В каждом опыте e_i имеет нормальный закон распределения.

2. В каждом опыте математическое ожидание e_i равно нулю.

3. Во всех опытах дисперсия e_i постоянна и одинакова.

4. Во всех опытах ошибки e_i независимы.

Помимо допущений необходимо выполнение следующих предпосылок: 

1. Матрица наблюдений X имеет полный ранг (rank(X)=p).

2. Структура модели адекватна истинной зависимости.

3. Значения случайной ошибки e_i не зависят от значений регрессоров x_i

4. Ошибки регистрации

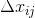
регрессоров пренебрежимо малы по сравнению со случайной ошибкой e. 

Пусть изменение выходной переменной y зависит от изменения переменных x₁, x₂, e и эта зависимость имеет вид: 

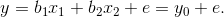
Располагая наблюдениями над контролируемыми переменными x₁, x₂, y, необходимо определить неизвестные коэффициенты b₁, b₂. В этом случае однозначность между x_j и y нарушается, т.к. имеет место ошибка e. Следовательно, точно определить коэффициенты b_j невозможно и определяются их оценки b₁, b₂

Для найденных оценок b₁, b₂ эмпирическое уравнение имеет вид: 

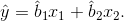
Для определения b₁, b₂ необходимо минимизировать сумму квадратов разностей 

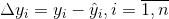
где y_i – значение выходной переменной в i-ом опыте; 

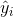
– значение, полученное из (1) путем подстановки x₁, x₂ в (1). 

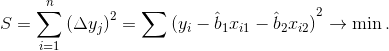
Функция (2) достигается при выполнении условий: 

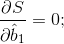
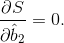
Продифференцируем S по b₁, b₂ и приравняем производные нулю:

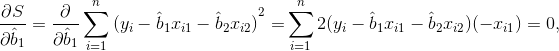
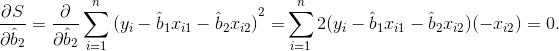
После преобразований получаем систему нормальных уравнений:

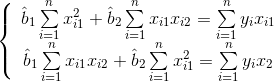
Для решения систем нормальных уравнений используем правило Крамера:

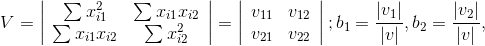
где V – информационная матрица; 
V_j (j=1,2)– матрица V, в которой j-й столбец заменен столбцом правой части системы (3). 

Решение существует, если rank(x)=2. Коэффициенты b₁, b₂ являются случайными величинами. Если в уравнение регрессии включить новую переменную, то необходимо будет коэффициент b_j вычислить заново.

В матричной форме обобщенное уравнение регрессии имеет вид Y=XB+E. 

Оценки B минимизируют сумму квадратов отклонений

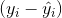
, т.е.: 

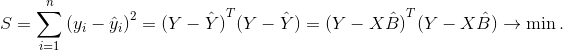
Раскрыв (4) и учитывая, что

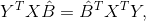
получим 

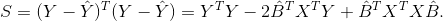
Продифференцировав S по

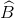
получим

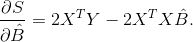
Приравняем данный результат к нулю, после чего получим систему нормальных уравнений, которая в матричной форме записывается как 

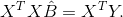
Из этой системы получаем решение для

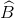
равное 

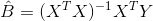
Полученная таким образом оценка называется оценкой наименьших квадратов или оценкой МНК. 

Для определения вектора необходимо по данным наблюдения найти матрицу, обратную к матрице X^TX, и вектор X^TY: 

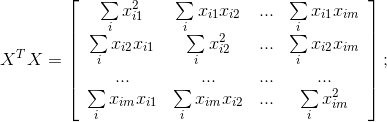
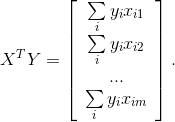
Обычно предполагается, что уравнение регрессии имеет свободный член, т.е. B₀. Для того чтобы получить оценку этого параметра (B₀), расширим матрицу X^TX, введя в нее переменную X_i0=1. Тогда матрицу X в развернутом виде можно записать как: 

откуда 

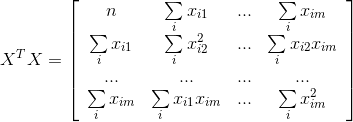
и

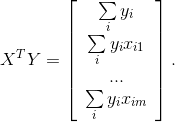
При соблюдении введенных допущений МНК оценки регрессионных коэффициентов  b_j являются несмещенными, состоятельными и эффективными. МНК не требует, чтобы все входные переменные X_j были распределены нормально, а лишь требует, чтобы при любом фиксированном наборе X_ij, выходная переменная y была распределена нормально. Это необходимо для корректной интерпретации результатов с использованием распределений Фишера и Стьюдента.