Математические модели задач дискретного программирования

Задача о контейнерных перевозках (задача о бомбардировщике или задача о рюкзаке). Контейнер имеет m отсеков вместительностью b_i, 

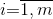
единиц для перевозки n видов продукции, которую можно брать в количестве 0,1,2 … единиц.

Пусть a_ij – затраты i-го отсека на перевозку единицы j-ї продукции, а c_j полезность единицы j-ї продукции. Необходимо найти такой план перевозки, который максимизирует общую полезность рейса. Обозначим через x_j количество единиц j-ї продукции, которая загружена в контейнер. Тогда модель задачи принимает вид 

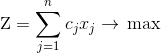
при условиях ограничений на вместительность отсеков 

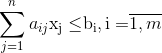
и неотъемлемость и целочисленности переменных 

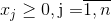
Частный случай этой задачи – задача о ранце, в который любой из заданного набора предметов можно выбрать (1) или нет (0). Следовательно, условие представленное выше заменяется

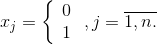
Задача о назначении (задача выбора)

Распределить n работ между n рабочими местами, причем на каждом из них можно выполнить любую из работ. Назначение i-ї работы j-му рабочему месту связанное с прибылью (или затратами) c_ij. Распределения нужно провести таким образом, чтобы суммарная прибыль (затраты) был максимальной (или затраты минимальными). Обозначим искомую переменную через x_ij, причем если i-й вид работы предназначенный j-му рабочему месту, то x_ij=1, и x_ij=0 в противном случае.

Математическая модель задачи такая:

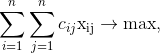
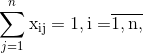
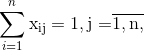
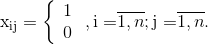
Транспортная задача с фиксированными доплатами

Пусть имеем m пунктов производства с объемами a_i,

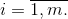
Нужно установить такие объемы перевозок x_ij к n пунктам потребления с объемами b_j, 

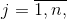
которые минимизируют целевую функцию

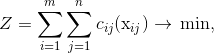
где 

с_ij(x_ij)=d_ij, если x_ij>0 и с_ij(x_ij)=0, если x_ij=0 

при условиях 

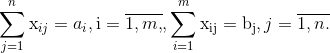
Здесь

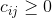
– транспортные затраты на перевозку единицы груза 

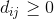
– фиксированные доплаты за аренду транспортных средств.

Задача о выборе транспортных средств

Разные типы самолетов гражданской авиации отличаются один от другого такими основными показателями как грузоподъемность, вместительность, себестоимость рейса. Выполняя рейс по i й авиалинии

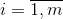
 каждый самолет j-го типа

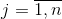
перевезет определенное количество пассажиров, грузов, почты. За время рейса он тратит определенное количество ресурсов (горюче и т.п.), которые составляют в стоимостном виде себестоимость рейса c_ij. Поскольку тарифная уплата за перевозку пассажира или единицы груза не зависит от типа самолета, то прибыль аэрофлота зависит от назначения самолетов на авиалинии. Поэтому оптимальным распределением самолетов по авиалиниям считают такой, при котором общая себестоимость минимальная во время выполнения плана перевозок. Обозначив через x_ij искомое количество самолетов j-го типа, которые предназначены на i-ю авиалинию, запишем математическую модель задачи

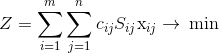
при условиях: 

— перевозка пассажиров

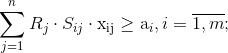
— перевозка грузов

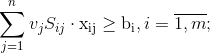
— перевозка почты

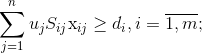
— количества действующих самолетов

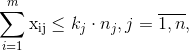
где R_j, v_j, u_j – количество пассажиров (вместительность самолета), грузов и почты, которые перевозятся самолетами j-го типа; a_i, b_i, d_i – количество пассажиров, грузов и почты соответственно, которые нужно перевезти по i-й авиалинии; n_j – количество самолетов j-го типа; k_j – коэффициент исправности самолета j-го типа, S_ij – максимальное количество рейсов, которые может выполнить самолет j-го типа на i-и авиалинии за определенный период.