Кроме метода отсечения, существует широкий класс довольно универсальных методов, основой которых является поиск оптимума на дискретном множестве планов задачи, на каждом шагу которого исключается из рассмотрения значительное количество неоптимальных планов. Такие методы называют методами веток и границ. Суть их в том, что множество планов задачи разбивают на ряд подмножества, для каждой из которых находят соответствующее решение. Процедуру повторяют до тех пор, пока не находят подмножество, которое содержит оптимальный план.
Процесс начинается с решения исходной задачи без целочисленности переменных. Если план Х* не удовлетворяет условие целочисленности, то значение целевой функции A = Z(X*) дает верхнюю оценку искомого решения (рекорд) на множестве планов задачи G0. Дробную базисную переменную, например, хl, в целочисленном плане нужно или уменьшить к [хl], или увеличить к [хl]+1.
Итак, промежуток [хl] ≤ хl ≤ [ хl]+1 не содержит допустимых целочисленных компонент решения. Таким образом, исходное множество планов задачи G0 разбивается на две подмножества
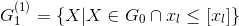
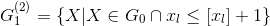
Находим решение и оценки на этих подмножествах. Если решений на
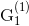
целочисленное, то оптимальным будет тот, в котором оценка A большая. Если же предположим, что множеству
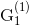
имеем целочисленный решения, а на
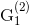
дробовой, но
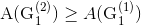
, то продолжаем разбивать подмножество
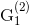
, поскольку на следующем шагу можем найти целочисленный план, оценка которого будет превышать оценку
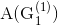
Этот процесс длится до тех пор, пока не будет найден целочисленный решений с максимальной оценкой.

