Общая задача нелинейного программирования заключается в нахождении определенного екстремума целевой функции
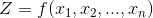
на множестве планов задачи, которая определяется системой условий
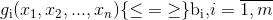
где все функции (или их часть) нелинейные. К представленным ограничениям могут быть отнесены ограничения на знак переменных, условие дискретности части или всех переменных.
Для некоторых типов задач нелинейного программирования разработаны определенные методы, которые дают возможность получить их точные решений, хотя могут возникнуть другие трудности, например, вычислительного характера. Основными свойствами задач нелинейного прораммирования, которые порождают трудности для создания эффективных методов их решения, есть наличие в некоторых задачах не одного, а нескольких экстремальных значений целевой функции; точка, которая является оптимальным планом задачи нелинейного программирования, может быть как внутренней, так и произвольной предельной точкой множества планов задачи; система условий может определять область существования планов задачи произвольной конфигурации, она может быть не выпуклой и даже состоять из нескольких отдельных не связанных между собой частей; требование дискретности, в частности, целочисленности решения; задача может содержать разрывные и многозначные функции.

